圆

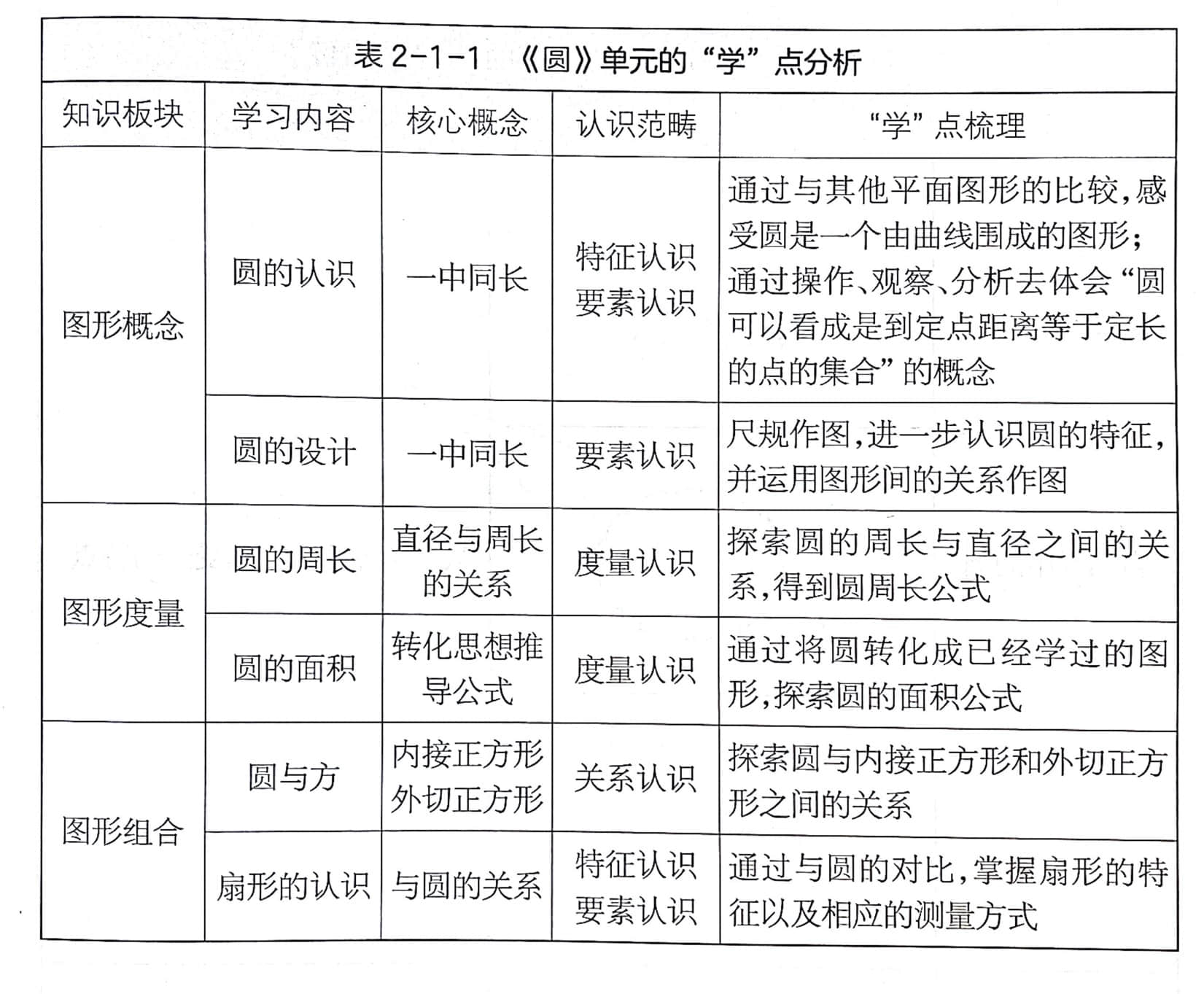
1 圆单元学点分析

《因用而学》P39

2 概念定义

姜荣富.展开基本概念的发生过程——数学知识的探求与创新意识的培养[J].小学数学教师,2022,No.390(04):46-49.

圆是最美的图形，是二维空间的完美形式，圆的美学价值体现在它的对称性上。把画圆的活动与理解圆的本质特征联系起来，即画圆时先画定长的线段，再跟随圆规针尖的转动想象定长线段旋转一周的过程，最后把画和想的过程陈述为发生式定义。

张奠宙教授建议，在使用圆规画圆之后，不妨提出如下定义：让线段OA绕着它的一个端点O旋转一周，我们把另一个端点A所画出的曲线叫做圆，点O称为圆心，OA称为半径。

3 S=πr2 读法

“πr的平方”，还是“π—r的平方”？（后者）

4 学生课前的画法

周月文.运用问题提出 促进深度学习——以“圆的认识”教学为例[J].小学数学教师,2022,No.391(05):38-43.

• （图2）我借助圆形盖子画出了圆。
• （图3）我用直尺也画出了圆。先确定好中心点和一个固定的长度，绕着中心点转动直尺，按固定长度一直画线段，当线段不断增加的时候，这个图形越接近于圆。
• （图4）我用一支笔固定线绳的一端，另一支笔把线绳拉直绕一圈，画出了一个圆。
• （图5）我用圆规有针尖的那一头抵着纸，有铅笔的那一头转一圈，画出了一个圆。

5 圆周率估算

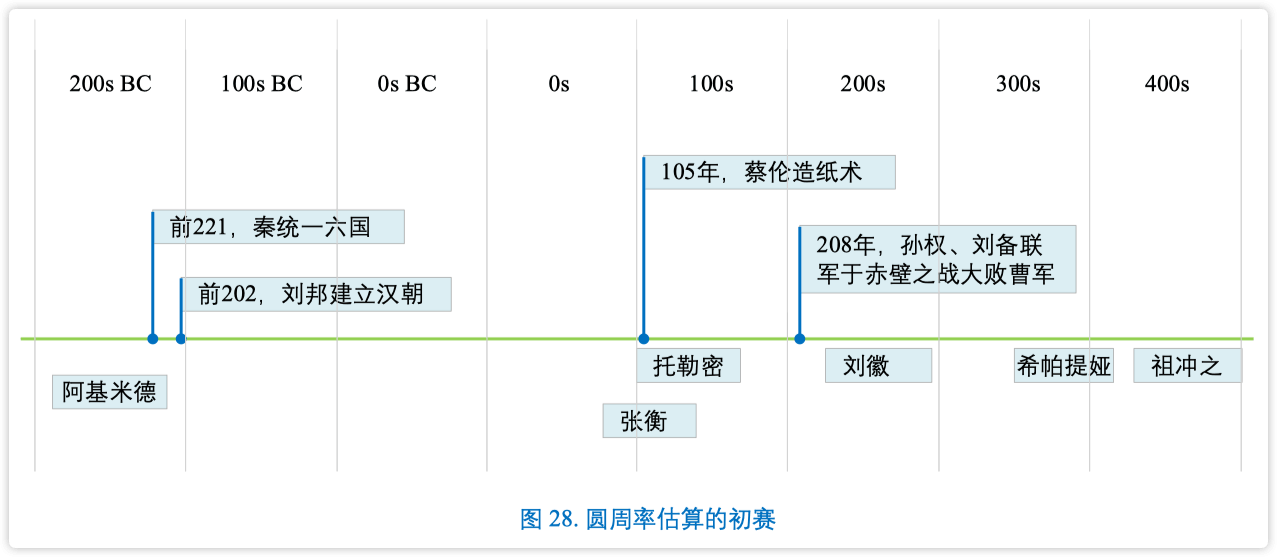
古希腊阿基米德，利用和圆内接正多边形和外切正多边形来估算 π。阿基米德最后计算到正 96 边形，估算圆周率在 3.1408 到 3.1429 之间。

中国古代魏晋时期的数学家——刘徽 (约 225 年 ~ 约 295 年) ——用不断增加内接多边形估算 圆周率，这种方法被称之为割圆术。

刘徽也用割圆术，从直径为 2 尺的圆内接正六边形开始割圆，依次得正 12 边形、正 24 边 形、正 48 边形等等。割得越细，正多边形面积和圆面积差别越小。用他的原话是“割之弥细，所 失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣。”这句话中，我们可以体会到“逼 近”、“极限”这两个重要的数学思想。

最后，刘徽计算了正 3072 边形的周长，估算得到的圆周率为 3.1416。

刘徽之后约 200 年，中国古代南北朝时期数学家祖冲之 (429 ~ 500) 也是用割圆术，最后竟然 达到正 12288 边形，估算圆周率为 3.1415926 到 3.1415927 之间。祖冲之再一次刷新圆周率记录， 而这一记录几乎保持一千年，直到新的估算圆周率的数学工具横空出世。

6 圆周率小数点后1000位

目前，背诵 pi 的小数点后最多位数的世界吉尼斯纪录是 70,000 位。该纪录由印度人在 2015 年创造，用时近 10 小时。

7 布丰实验

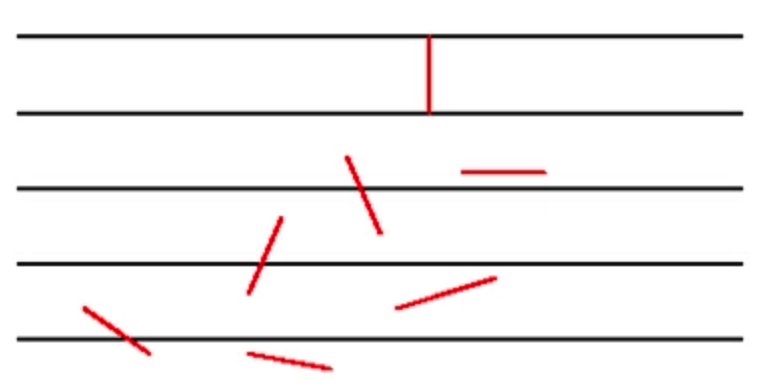
18世纪，蒲丰提出以下问题：设我们有一个以平行且等距木纹铺成的地板（如概述图），随意抛一支长度比木纹之间距离小的针，求针和其中一条木纹相交的概率。并以此概率，布丰提出的一种计算圆周率的方法——随机投针法。这就是蒲丰投针问题（又译“布丰投针问题”）。

请 Ta 喝咖啡 ☕️

喝咖啡记录：